sunniva@ngi$ echo $(whoami)

Problem

Optimization: an act, process, or methodology of making something (such as a design, system, or decision) as fully perfect, functional, or effective as possible
specifically : the mathematical procedures (such as finding the maximum of a function) involved in this

Curve Fitting: the empirical determination of a curve or function that approximates a set of data
Merriam-Webster Dictionary

A solution

Another solution

A third solution

Choose your model

Real (NGI work) life example

Real (NGI work) life example

Horizontal displacement curves under load

What is Curve Fitting?

• Find the best-fit curve for a dataset using a known model
  • Minimize the difference between observed and predicted values

• Categories of problems
  • Linear vs non-linear

  • Unconstrained vs Constrained

Difference between observed and predicted values

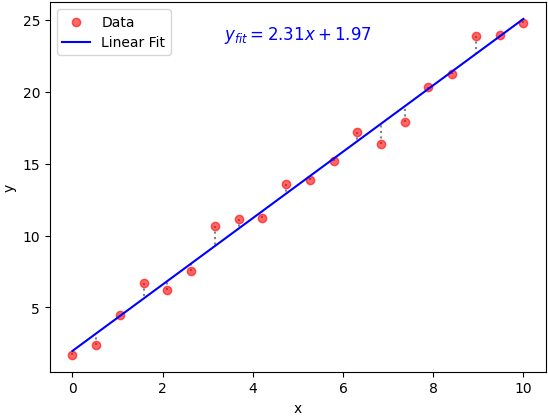
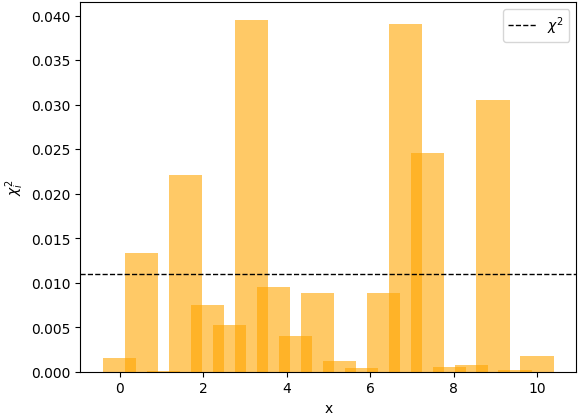
Curve fitting requirements

• Estimate parameter uncertainties
• Support non-linear problem solving
• Easily change optimization algorithm
• Provide high-level tools for setting parameter bounds

Recommended tool (by me)

Topic	Details
Library Name	lmfit
Description	High-level interface to non-linear optimization and curve fitting problems
GitHub Stars	1.1k
Last Commit Date	13.10.2024 (on 22.10.2024)
Built On	SciPy’s curve_fit

A new non-linear problem

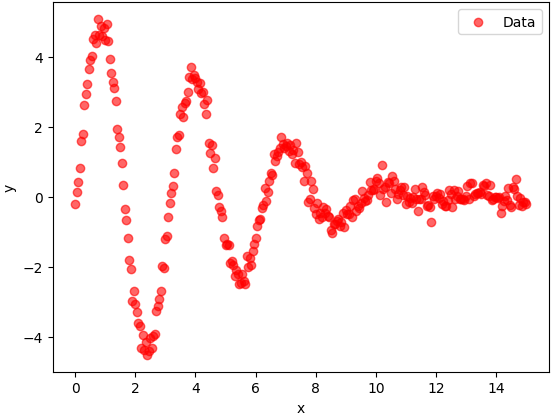Let's see some code

Problem setup

from lmfit import Minimizer, create_params

def residual(parameters, x, data):
    model = (
        parameters["amplitude"]
        * np.sin(x * parameters["omega"] + parameters["phi"])
        * np.exp(-x * x * parameters["gamma"])
    )
    return model - data

parameters_initial = create_params(
    amplitude=10,
    gamma=0.1,
    omega=3.0,
    phi=0.0,
)

minimizer = Minimizer(residual, parameters_initial, fcn_args=(x, data))
result = minimizer.minimize(method="least_squares")

Handling bounds

from lmfit import Parameters

params = Parameters()
params.add('amplitude', value=10, min=0)
params.add('gamma', value=0.1)
params.add('phi', value=0.0, min=-np.pi/2., max=np.pi/2.)
params.add('omega', value=3.0)

from lmfit import create_params

params = create_params(amplitude=dict(value=10, min=0),
                       gamma=0.1,
                       omega=3,
                       phi=dict(value=0, min=-np.pi/2, max=np.pi/2))

Interpret simulation results

[[Fit Statistics]]
    # fitting method   = least_squares
    # function evals   = 58
    # data points      = 301
    # variables        = 4
    chi-square         = 12.1867036
    reduced chi-square = 0.04103267
    Akaike info crit   = -957.236198
    Bayesian info crit = -942.407756
[[Variables]]
    amplitude:    5.03088066 +/- 0.04005821 (0.80%) (init = 10)
    gamma:  0.02495457 +/- 4.5396e-04 (1.82%) (init = 0.1)
    omega:  2.00026311 +/- 0.00326183 (0.16%) (init = 3)
    phi: -0.10264955 +/- 0.01022294 (9.96%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(omega, phi) = -0.7852
    C(amplitude, gamma)   = +0.5840
    C(amplitude, phi)   = -0.1179

Demo